Solving Linear Systems
Define a matrix
A = [1 2 5; 4 5 6; 7 8 9]
A =
1 2 5
4 5 6
7 8 9
and a right-hand side (column) vector
b = [2 5 7]'
b =
2
5
7
To solve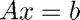 
for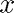 
we type
x = A\b
x =
-2.1667
3.3333
-0.5000
Check the answer
A*x-b
ans =
1.0e-015 *
0.4441
-0.8882
0
Define another (singular) matrix
A = [1 2 3; 4 5 6; 7 8 9; 10 11 12]
A =
1 2 3
4 5 6
7 8 9
10 11 12
rank(A)
ans =
2
and a right-hand side (column) vector
b = [2 5 7 8]'
b =
2
5
7
8
Now the (least-squares) solution is given by
x = A\b
Warning: Rank deficient, rank = 2, tol = 1.4594e-014.
x =
-0.2500
0
0.9167
Note that 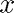does not satisfy the linear system
A*x-b
ans =
0.5000
-0.5000
-0.5000
0.5000