Function Handles and Function Functions

The name of an anonymous function is known as a function handle.

We can define

sqr = @(x) x.^2

sqr = 

    @(x)x.^2

Note that this function will operate elementwise on vectors or matrices. For example

sqr(5)

ans =

    25

sqr(1:5)

ans =

     1     4     9    16    25

Another example with a random $2\times 2$ matrix

A = floor(10*rand(2,2))
A_squared = sqr(A)

A =

     8     1
     1     5


A_squared =

    64     1
     1    25

MATLAB includes many so-called ''function functions''. These are functions that take function handles as input. Examples are

quad (for numerical integration),
certain calculus-related routines (such as fminbnd or fzero),
and many commands for the solution of differential equations (such as ode45 or ode15s).

Of course, you can also write your own function functions.

We now give three examples.

Numerical Integration:

To integrate the function 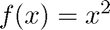$f(x)=x^2$ on the interval $[0,1]$ we can pass the function handle sqr defined above to the MATLAB quad function

quad(sqr,0,1)

ans =

    0.3333

To find the minimum of the function 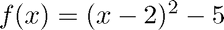$f(x)=(x-2)^2-5$ on the interval $[-3,3]$ we can define a new function handle and then pass it to fminbnd.

sqr2 = @(x) (x-2).^2-5
disp('The minimum occurs at')
fminbnd(sqr2,-3,3)
disp('and its value is')
sqr2(ans)

sqr2 = 

    @(x)(x-2).^2-5

The minimum occurs at

ans =

     2

and its value is

ans =

    -5

To find the zeros of the function 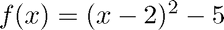$f(x)=(x-2)^2-5$ on the interval $[-3,3]$ we can use the function handle just defined together with fzero.

fzero(sqr2,-3,3)

ans =

   -0.2361

Here is a plot of this function

ezplot(sqr2,[-3,3]); grid on

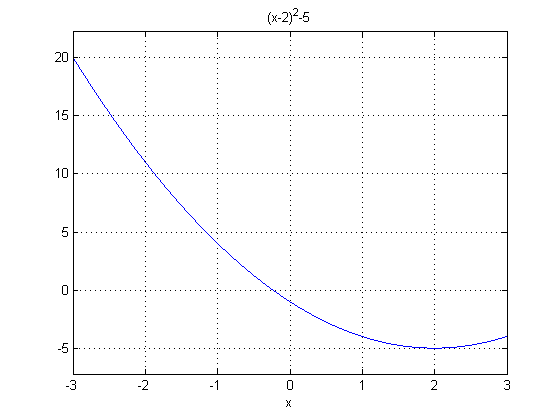
or - using the standard plot command:

x = linspace(-3,3,100);
figure; plot(x,sqr2(x)); grid on